Unfair Randomness with Inverse Transform Sampling
Frac is a game about fractions between 0 and 1. It generates numerators and denominators at random, but unfairly. It is more likely to pull larger denominators (up to the current maximum).
To do this, I used inverse transform sampling. Inverse transform sampling is a neat way to generate samples from any distribution given uniform random samples. For some distributions the math can get pretty complicated, but for generating numbers according to simple rules like this, it doesn't have to be.
Let's call the maximum denominator D. Then the distribution or PDF (probability density function) could look like
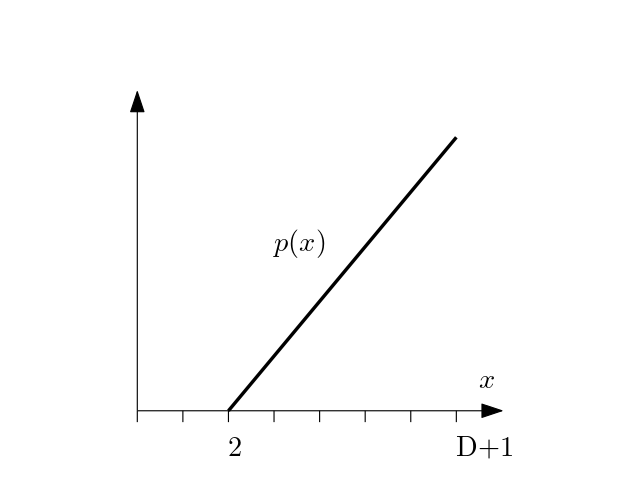
where the horizontal axis represents the denominators and the vertical axis represents the probability of pulling that denominator. It's just an upward line, so the larger the value, the more likely it is. We'll round down to get an integer and our random number generator returns values in [0, 1); that's why it goes to D+1 instead of D. We don't care about the height or slope of the line for now, just the shape.
From this we can get our CDF (cumulative density function), which is the integral of the PDF. The integral of a line is a parabola, so the CDF looks like
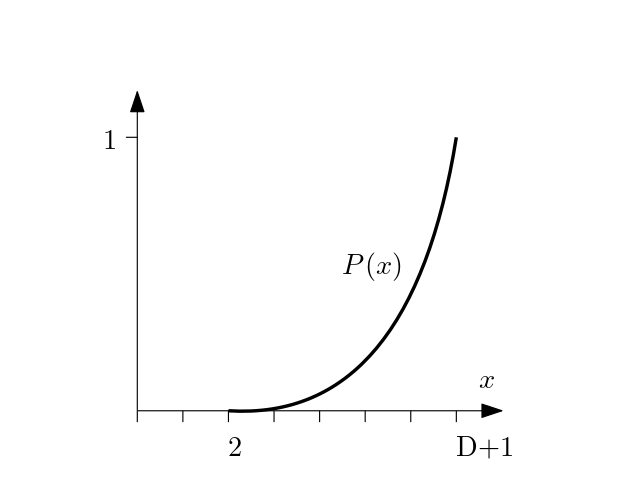
where the vertical axis represents, for the value on the horizontal axis, the probability of pulling that or any smaller number. The probability of pulling a number smaller than 2 is 0. The probability of pulling a number smaller than D+1 is 1. In other words, there is a 100% chance to pull a number less than D+1, and a 0% chance it is less than 2. Again, we'll round down, hence D+1.
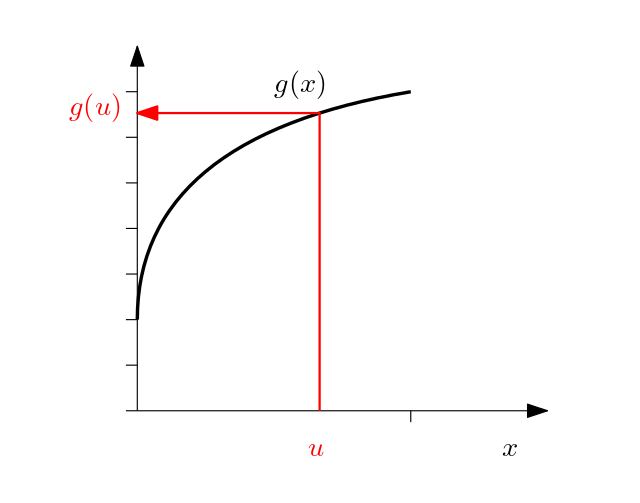
We need the inverse of this function. So we flip the axes:
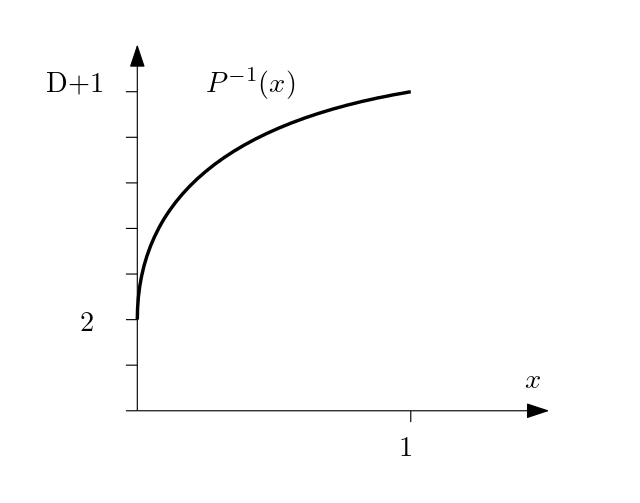
which is a square root. From the endpoints (0, 2) and (1, D+1) we can take the basic square root function f(x) = sqrt(x), with f(0)=0 and f(1)=1, and stretch it out vertically by D-1 (the distance from 2 to D+1) and shift it up by 2 to get a new function g(x) = (D-1) sqrt(x) + 2.
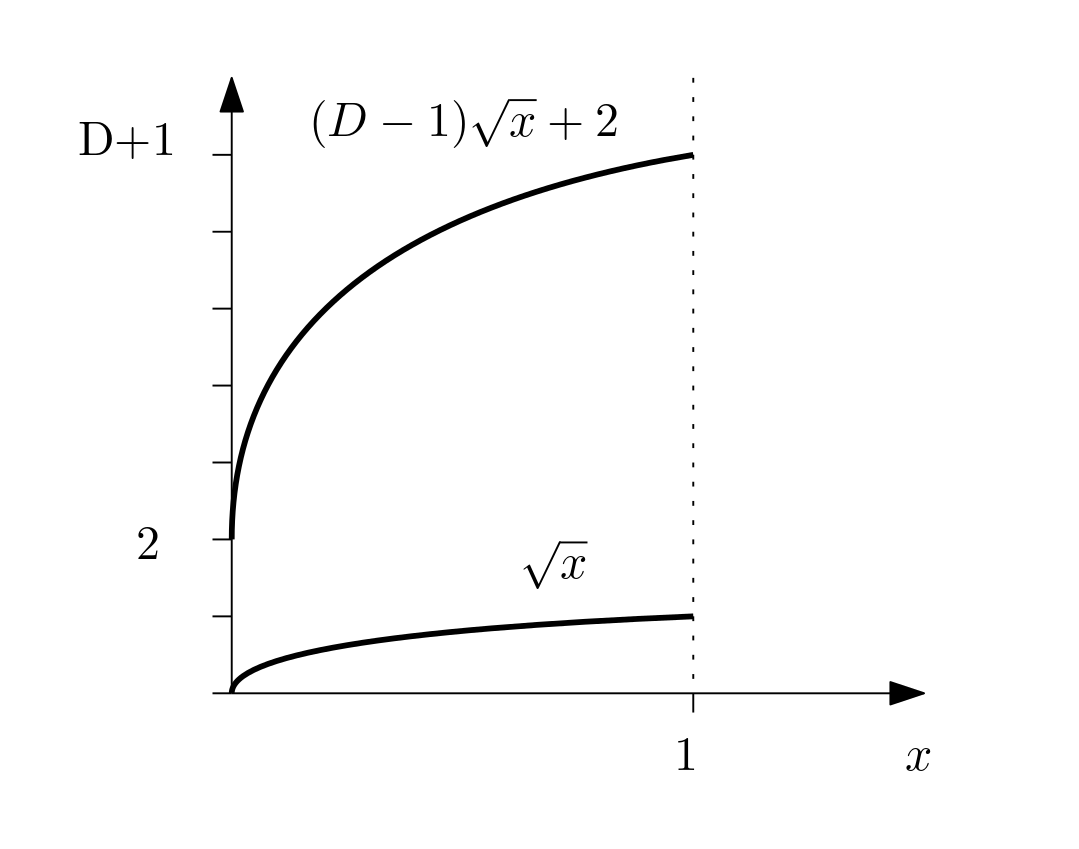
and that's pretty much it. Get a random sample from [0,1), plug it in for x in g(x), and what comes out will be a new random value in [2, D+1), probably closer to D+1 than to 2.
The code might look like:
u = Math.random();
d = Math.floor( 2 + Math.sqrt(u) * (D - 1) );
I hope you found this useful and informative. There's plenty more that can be done with inverse transform sampling; this was just a simple example. You can learn more about it on Wikipedia.
Frac
Practice fractions by playing Pong
| Status | Released |
| Author | phlp |
| Genre | Educational |
| Tags | Math, numeracy |
| Accessibility | Interactive tutorial, Textless |
Leave a comment
Log in with itch.io to leave a comment.