Tangent of π/8
While working on the camera logic for Counting, I came across the neat fact that the tangent of π/8 (half of 45°) is exactly the square root of 2 minus 1:
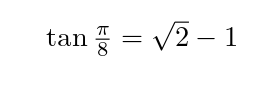
I searched and found a couple of proofs of this, both using trigonometric identities (gross) and one even got the wrong answer. So I came up with this proof using triangles.
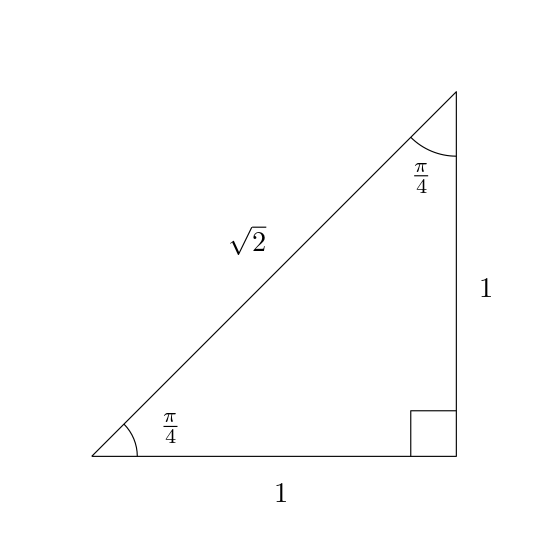
Start with an isosceles right triangle, i.e. one with angles 45-45-90, and the matching sides length 1. The hypotenuse has length sqrt(2).
Draw another isosceles triangle inside this one:
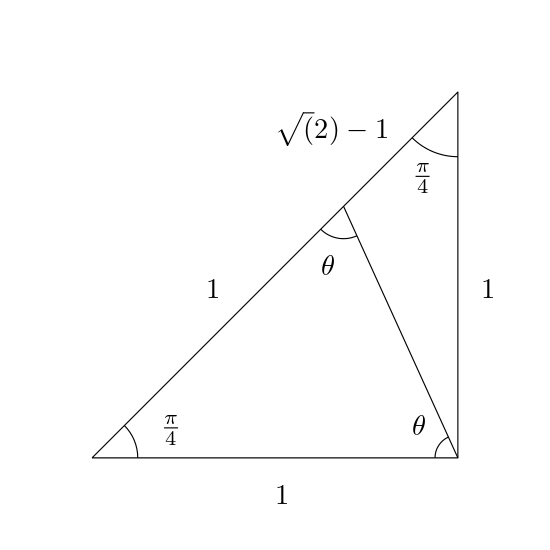
This divides the hypotenuse into two sections: from one of length (sqrt2) into one of length 1 and one (sqrt(2)-1). We won't worry about what theta is. Let's draw another isosceles triangle, this time on the outside of this one:
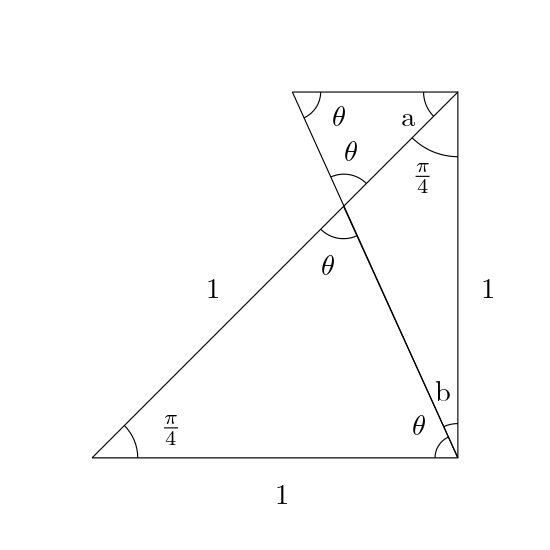
The angles theta are the same in both triangles because two of them are opposite, i.e. they're on opposite sides of intersecting lines. So what about the angles a and b? a has to be the same as the bottom-left angle, π/4, because they're in similar triangles (triangles of different size but the same angles). As for b, we can use the fact that it's part of a right angle with theta:

And then use the smaller triangle containing b (whose angles have to add up to 180° or π) to get another equation:
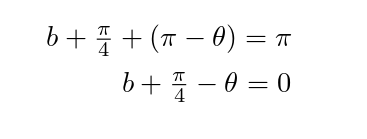
Add these two together to cancel out theta and leave 2 b = π/4, or b = π/8. Pull out this one triangle:

aaaaand we're done. Tangent is the length of the opposite side divided by the length of the adjacent side:
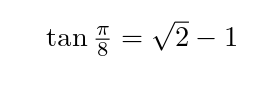
Counting
Counting in a decimal number system
| Status | Released |
| Author | phlp |
| Genre | Educational |
Leave a comment
Log in with itch.io to leave a comment.